Some result of the nonlinear Swarchschild toy case

Newton convergence comparison

This problem is a toy problem to see what optimization could be optain be the use of a Newton Krylov method and compare this to the default Newton raphson approaches of the Kadath librairy. A small size system was used, keeping in mind that Krylov method are generally favorable to large system.

The comptation was made on a computeur Intel(R) Core(TM) i7-7700T CPU @ 2.90GHz, with a stopping tolerance of \(1. e^{-5}\) on the scaled maximum norm and on the step norm of the system function \(F(u)\). Here is the print of each test :

Classical Newton Raphson

syst.neq =9
Size = 255
tol = 1e-5

Newton iteration 4
9.18397e-07
elapsed time: 23.8314s
Error max 0.0016278

Optimize Newton Krylov

syst.neq =9
Size = 255
Flag globalstrategy = 0 (0 = None, 1 = Linesearch)
Linear solver is SPBCG with maxl = 15, maxlrst = 2
Preconditioning uses full matrix inversion at first
Tolerance parameters:  fnormtol = 1e-05   scsteptol = 1e-05

elapsed time: 7.75441s
Computed solution (||F|| = 7.42246e-06):

Final Statistics :
nni    =     3    nli   =     3
nfe    =     4    nfeSG =     9
nps    =     9    npe   =     1     ncfl  =     0

Error max 0.00133879

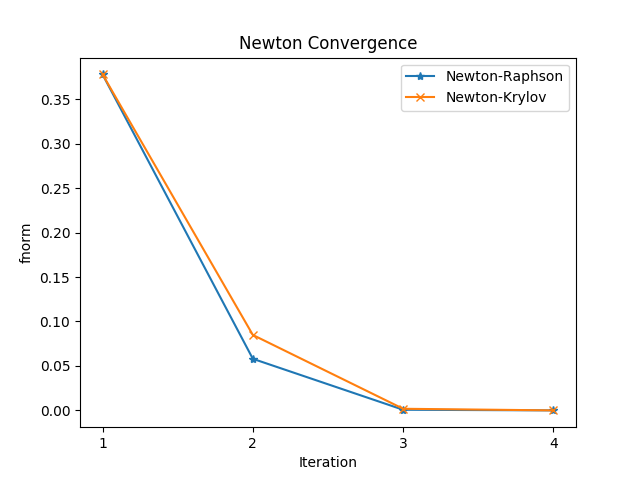
f norm over Newton iterations for nbr = 5, i.e. a system size of 255 and 9 equations. Comparison between the classical Newton-Raphson and the Newton-Krylov methods.

The figure [fig_Newton_iter] show the comparison of both method for a size problem of 255, which correspond of \(9\) Kadath equations. For both method, the solution involved \(4\) Newton iterations to reach the given tolerance. In the Kylov method, a total of \(9\) function evaluations for Jv evaluations, which correspond to an average of about \(2\) Krylov iterations per Newton iteration. The statistics printed for the Newton Krylov method are the total numbers of nonlinear iterations (nni), of func evaluations (excluding those for Jv product evaluations) (nfe), of func evaluations for Jv evaluations (nfeSG), of linear (Krylov) iterations (nli), of preconditioner evaluations (npe), and of preconditioner solves (nps). All of these optional outputs and others are described the Kinsol library [2].

We can see a gain of factor \(3\) by the use of the Newton Krylov method instead of the Newton Raphson. This is confirmed by the scaling in figure [fig_Newton_iter] below.

Matrix size scaling comparison in serial

Increasing the size of the problem matrix and compare. See figure below.

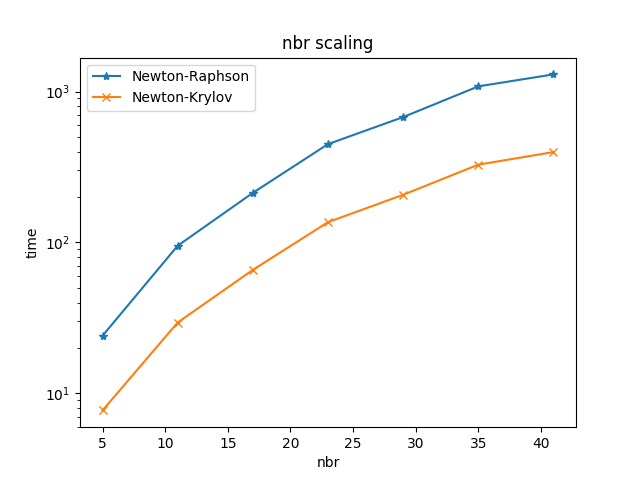
f norm over Increasing the size of the problem matrix and compare. Comparison between the classical Newton-Raphson and the Newton-Krylov methods.

The average gain factor is \(3.247\) between the classical Newton-Raphson and the Newton-Krylov methods.

conclusion

We show in this work that a Newton-Krylov approaches can gives better results that a traditional Newton Raphson approaches, with a gain of about \(3\). This use a non optimize Preconditioning matrix, but with a smart optimization of the different steps of his computation. This could be even more efficient by the use of a block diagonal approaches with a defined domain. This could be optimize for a particular physical problem using its particularities by an approximate linearized analytical solution for example. This is also possible to define advance preconditionner based on Multigrid or using another domain discretization process.

To extend this method to parallel resolution, some advance work needs to be done in Kadath to structure the vector solution used in the spectral method, and thus exploit the advantages of a parallel preconditioner.