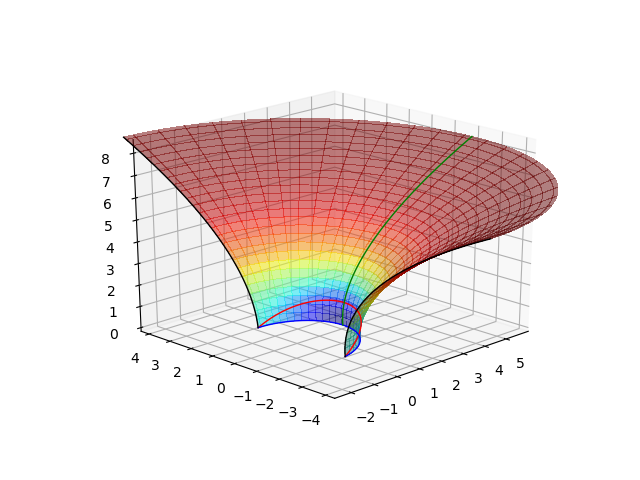
Isometric Embedding

Posted on June 12, 2021  •  1 minutes  • 175 words

Description

In the (Chantry et al. 2021 7) paper, we propose two approaches to obtain an isometric embedding of the poloidal Kerr sub-manifold. The first one relies on the convex integration process using the corrugation from a primitive embedding. This allows us to obtain one parameter family of embeddings reaching the limits of an isometric embedding. The second one consists in consecutive numerical resolutions of the Gauss-Codazzi-Mainardi and frame equations. This method requires geometric assumptions near the equatorial axis of the poloidal sub-manifold to get initial and boundary conditions. The second approach allows to understand some physical properties in the vicinity of a Kerr black hole, in particular the fast increasing ergoregion extent with angular momentum.

The Isopol program contains solver for the last approach. This include solvers for CGM and Frame equations with no specific librairy dependances.

Project Website

See Isopol project website for more information.

Related Article