The retrograde rotation of Venus

This page is available in French

This is a dicactical account of the common work with Alexandre Correia (Observatoire de Paris et Université d’Aveiro, Portugal) on the long term evolution of Venus rotation.

1. The rotation period of Venus

Because of the thick cloud cover on the surface of Venus, its rotation period remained unknown for a long time. The discovery of the red Jupiter spot, and the superficial structure of Mars made possible for Jean-Domenica Cassini (1625-1712) to determine with a good precision the period of rotation of Jupiter and Mars since 1664-1666. But the exercise proves more difficult for Venus, not easily observable during several hours in continuity, and without apparent marks on its surface. The first observations of Jean-Domenica Cassini in 1666 and 1667 suggested him a period of less than one day, but did not allow to distinguish if the planet was in rotation or libration. A few years later, following observations carried out in 1726-1727, Francesco Bianchini (1662-1729) proposes a period of 24 days and 8 hours, whereas Jacques Cassini (1677-1756) finds 23h 15mn after a new analysis of the observations of his father, and shows that a period of 23h 20mn makes it possible to also account for the observations of Bianchini. The 23 hours period is confirmed by Francesco de Vico (1805-1848) which obtains the incredibly precise value of 23h 21mn 21.934s, after an observation campaign carried out between 1839 and 1841, during which he could follow planet in full day. The controversy will continue during more than one century between the partisans of Cassini for which the period of rotation was close to 23 h, and those of Bianchini which preferred to see planet turning around its axis in 24 days.

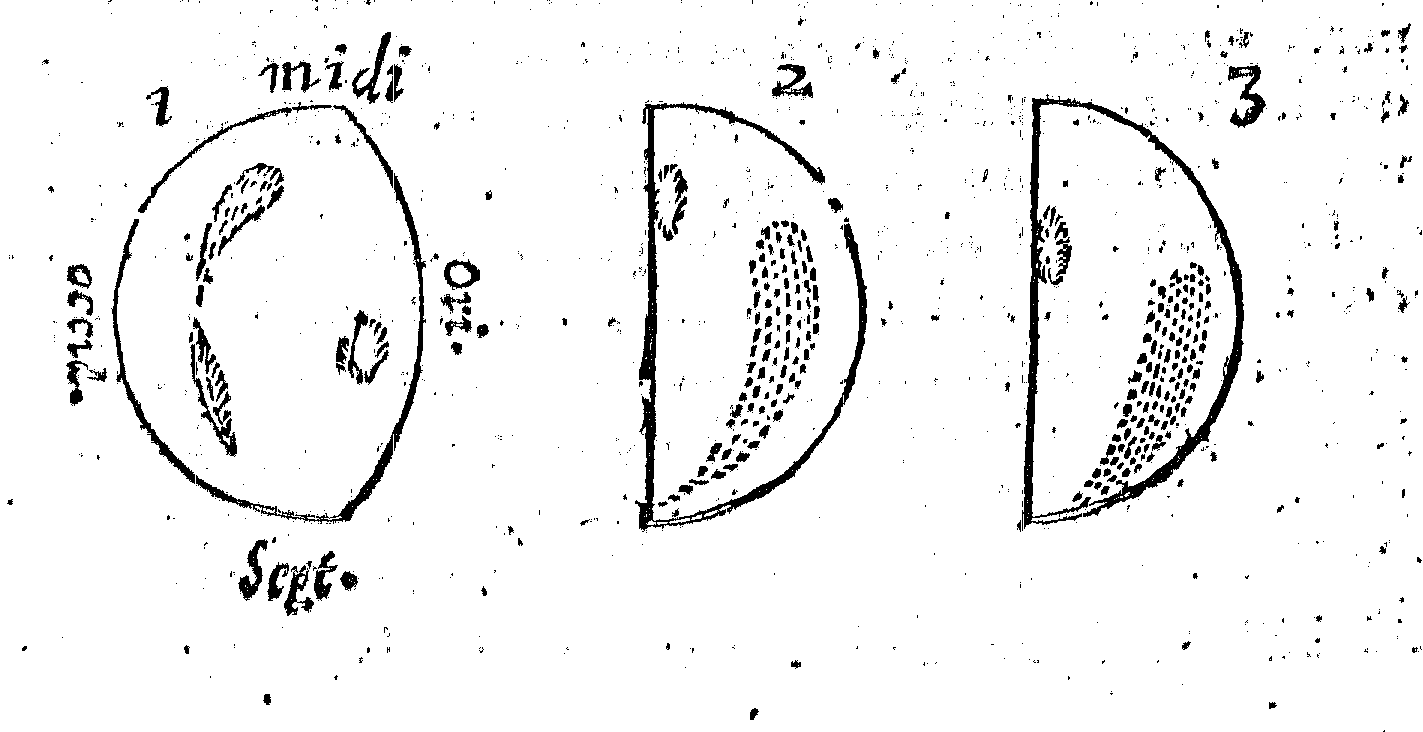
Figure.1 : Observation of Venus by Jean-Domenica Cassini in February and April 1667. “Until the 28 day of April, I could not notice any shiny spot similar to that which I had already seen, but this day, fifteen minutes before the rising of the Sun, I started to re-examine the disc of this Planet, for which half or approximately appeared at the time enlightened, a shiny spot located near the section” (Gallica/BNF).

On the other hand, Giovanni Virginio Schiaparelli (1835-1910), during its observations of 1877-1878, does not note significant variation of the rotation of planet, and concludes that its period of rotation cannot be of 23h, but must be much longer. He proposes then in 1890 a period of 224,7 days for Venus rotation, corresponding to a state of synchronous rotation with its orbital motion around the Sun, just like the Moon carries out a rotation on itself in the same time as its revolution around the Earth. In this configuration, for a Venusian, the Sun appears fixed in the sky, and half of planet is plunged in the night, while other half profits of a perpetual sun. The proposal of Schiaparelli renewed the controversy, and the observations of Venus continued. Camille Flammarion from its observatory of Juvisy observes the planet between 1887 and 1894, and publishes its conclusions in 1894. He does not manage to determine with precision the period of rotation, but concludes “that it is not very distant from twenty-four hours”. He observes even polar caps on Venus which enable him to say that the axis of planet is not very tilted…

In fact, the true period of rotation of Venus will be discovered only in 1962, thanks to the radar observations carried out by the Jet Propulsion Laboratory (the USA) which make it possible to be freed from the cloud cover. These observations will show, at the great surprise of astronomers, that this planet has a retrograde rotation with a 243,0 days period (Goldstein, 1964, Carpenter, 1964). This period of rotation, associated to a 224,7 days orbital period leads to a duration of the Venusian “day” of 116 terrestrial days, with a Sun which rises to the west and sets in the east.

2. Tidal effects

The unusual Venus rotation results from an equilibrium between tidal friction effects resulting from body tides, and thermal atmospheric tide (Gold and Soter, 1969). In the case of the body tides, the Sun deforms planet and creates a bulge in the direction of the Sun (and opposite direction), but if the planet rotates more rapidly on itself than its revolution around the Sun, this bulge is shifted from the subsolar point, because the nonelasticity of planet does not return immediately in the direction of the Sun. There results an offset (delta) (fig. 2) between the bulge and the direction of the Sun, which induces a restoring torque on the rotation of the planet having for effect to slow it down. This effect will last as the rotation rate of planet is higher than its revolution around the Sun and will thus tend to bring planet in a synchronous state with its orbital period (as in the Earth-Moon system). If this effect had been the only present, the prediction of Schiaparelli would have been verified.

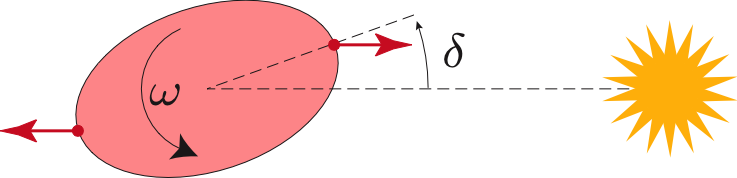
Figure.2 : Effect of solid tides exerted by the Sun on Venus.

Actually, in the case of a planet with a thick atmosphere like Venus, a second tidal effect is to be taken into account: the effect of thermal atmospheric tides (fig. 3). In this case, the Sun heats the atmosphere at the subsolar point, and to balance the pressures, then occurs a redistribution of the mass of the atmosphere in the more distant areas, with an important component perpendicular to the direction of the Sun. Here still, if the rotation of planet is faster than its revolution around the Sun, there will be a shift (delta) between the orientation of this atmospheric tidal bulge and the perpendicular with the direction of the Sun. If delta < 90°, this bulge induces an accelerating torque for the rotation of planet. When this torque is sufficiently important, as it is the case for Venus, the synchronous equilibrium becomes unstable, but appear two new equilibrium configurations, one prograde, and the other one retrograde (Correia and Laskar, 2001).

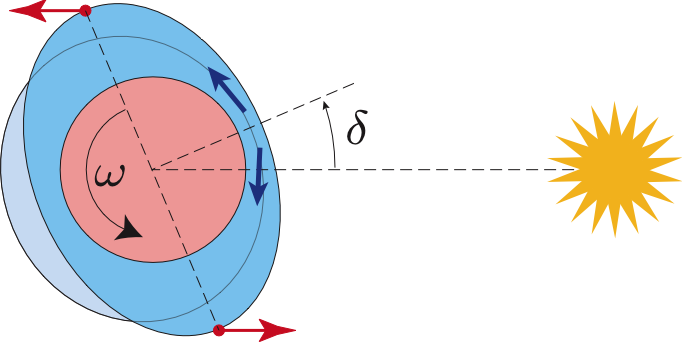
Figure.3 : Effect of solid tides exerted by the Sun on Venus.

3. The four final Venus states

The remaining question is to know under which initial conditions (period of rotation, and orientation of the axis at the end of the phase of formation of the solar system) a planet can reach such an equilibrium state?

One can show that for a large amount initial conditions, under the effect of tidal forces, but also of the dissipation that occurs at the core-mantle border, the obliquity of the planet (angle between the plane of equator and the orbital plane) will slowly evolve towards 0 or 180 degree, while its rotation reaches an equilibrium position under the various tidal torques, with only four possibility, two correspondant to a prograde state (F0+, Fp+) and two with a retrograde state (F0-, Fp -) (fig. 4). Once the rotation period of one of the final states is known, one can deduce the rotation period of the three others. Assuming that the current state is close to equilibrium, one can then deduce that the two retrograde states have 243.0 days period, and the two prograde states 76.8 days period.

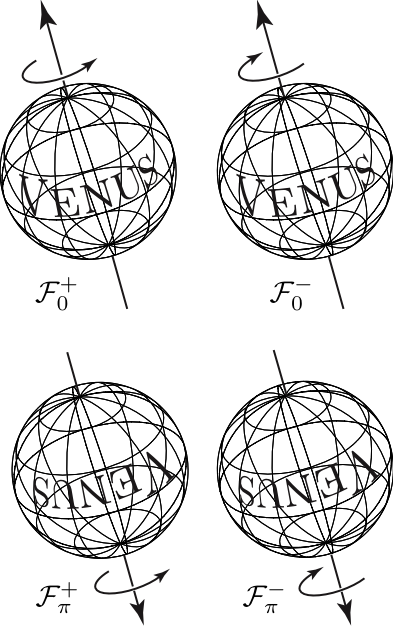
Figure.4 : The four final Venus states.

It should be stressed that retrograde states F0- and Fp- correspond both to the current observation of planet, but with completely different histories: in the first case, (F0 -), the planet, supposed to be initially in prograde rotation, will slow down under the influence of the dissipative effects, while its obliquity evolves to zero degree, then it stops its rotation, and starts to turn in the opposite direction to reach its final 243 days final period. In the second scenario, (fig. 5), the planet which can be initially with an obliquity of almost 0 degrees, will see its obliquity increasing considerably under the influence of the planetary perturbations, at the point of being able to be turned over, while slowing down, for finally reaching also a retrograde final rotation period of 243 days..

4. The chaotic obliquity of Venus

In figure 5, the frequency of precession of the axis of rotation of Venus is traced according to its obliquity. The trajectory corresponds to an initial obliquity of 1 degree and initial period of 3 days. This corresponds to a precession frequency of approximately 16 seconds of degrees per annum (81 000 years period). The precession is then in resonance with the oscillations of the plane of the orbit of the planet resulting from the gravitational perturbations from the other planets. These perturbations produce a very broad zone (in grey in the figure) in which the movement of the axis of planet will be chaotic, and can undergo very strong oscillations that may bring the obliquity beyond 70 degrees (the Earth would currently be in this situation in the absence of the Moon) (Laskar and Robutel, 1993).

Once that the obliquity reaches a large value, the dissipative effects of tidal and core-mantle friction can make the planet turn over, and bring it in the retrograde state Fp-. Because of the existence of this chaotic zone, which is crossed by the axis of planet during its history, all the initial conditions can lead to one of the four final states $({\cal F}0^+, {\cal F}{\pi}^+,{\cal F}0^-,{\cal F}{\pi}^-)$. The unusual Venus rotation thus does not require the assumption of a strong impact at the end of the formation of the Solar system which would have made the planet turn over, as it was sometimes proposed. In fact, by taking into account only dissipative effects of tidal and core-mantle friction, a large part of the acceptable initial conditions lead Venus to the current state, whatever its initial obliquity, but they are two possible scenarios leading at the same final apparent state.

• In the first case, the planet slows down, stops, and starts again in the other direction, whereas its obliquity tends towards 0°.
• In the second scenario, the planet is turned over and finishes with an obliquity of 180°.

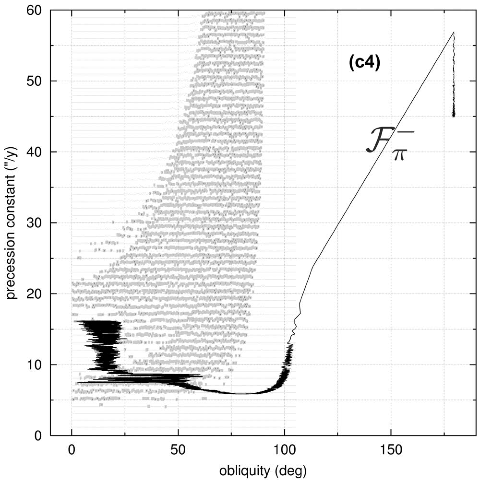
Figure 5 : Possible example of evolution of the Venus obliquity during its history. The frequency of precession (in seconds of arc per annum) is traced according to the obliquity of the axis (in degrees). The initial obliquity is one degree, and initial period of three. The frequency of initial precession is 16 seconds of degrees per annum, but because of dissipative effects of tidal and core mantle friction, the planet slows down and the frequency of precession decreases. The obliquity enters a very important chaotic zone then (in grey), resulting from the planetary perturbations. The obliquity can then strongly increase, until the dissipative effects lead it away from the chaotic zone, for a strong value of the obliquity. The various dissipative effects can then bring the obliquity towards 180 degrees (Correia and Laskar, 2003).

We thus end to a form of paradox where the retrograde rotation of Venus is the most probable result of a natural evolution, and not the result (always possible) of a strong accidental collision; but in same time, for a large part of the prograde initial conditions, it is possible to arrive in this state by two entirely different ways, that are not possible to distinguish with the observation of the present final state of the planet (Correia and Laskar, 2001).

5. References

• Carpenter, R. L. : 1964, Study of Venus by CW Radar, Astron. J. 69, 2
• Correia, A., Laskar, J.: 2001, The Four final Rotation States of Venus, Nature, 411, 767-770, 14 june 2001
• Goldstein, R. M. : 1964, Venus Characteristics by Eart-Based Radar, Astron. J. 69, 12
• Gold, T., et Soter, S. 1969. Atmospheric tides and the resonant rotation of Venus. Icarus 11, 356-366.
• Laskar, J., Robutel, P. 1993. The chaotic obliquity of the planets. Nature 361, 608-612.

(© J. Laskar, IMCCE/CNRS, Observatoire de Paris, last revision june 22, 2004)